Статистические характеристики

Одна из основных задач статистики как раз и состоит в надлежащей обработке информации. Конечно, у статистики есть много других задач: получение и хранение информации, выработка различных прогнозов, оценка их достоверности и т. д. Ни одна из этих целей не достижима без обработки данных. Поэтому, первое, чем стоит заняться — это статистическими методами обработки информации. Для этого нам будут нужны новые термины, принятые в статистике.

Мы будем использовать термины из первого столбца. Термины из третьего столбца могут встретиться вам в других учебных пособиях или справочниках по статистике.

Вернемся к выборкам и рядам данных. У каждой выборки есть своего рода «паспортные данные», которые весьма существенны. Следует только точно понимать, что они в принципе не могут дать полной информации о выборке: абсолютно полной информацией о выборке является сама выборка.

Итак, перейдем к составлению паспорта выборки.

Средним арифметическим ряда чисел называется частное от деления суммы этих чисел на их количество. Среднее арифметическое является важной характеристикой ряда чисел но иногда полёзно рассматривать и другие средние.

Модой называют число ряда, которое встречается в этом ряду наиболее часто. Можно сказать, что данное число самое «модное» в этом ряду. Такой показатель, как мода, используется не только для числовых данных. Вы уже знакомы с социологическими опросами. Если, например, опросить большую группу учеников, какой школьный предмет им нравится больше всего, то модой этого ряда ответов окажется тот предмет, который будут называть чаще остальных.

Мода—показатель, который широко используется в статистике. Одним из наиболее частых использований моды является изучение спроса. Например, при решении вопросов, в пачки какого веса фасовать масло, какие открывать авиарейсы и т. п., предварительно изучается спрос и выявляется мода — наиболее часто встречающийся заказ.

Заметим, что в рядах, рассматриваемых в реальных статистических исследованиях, иногда выделяют больше одной моды. Когда в ряду много данных, то интересны бывают все те значения, которые встречаются гораздо чаще других. Их статистики тоже называют модой.

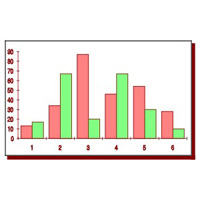
Однако нахождение среднего арифметического или моды далеко не всегда позволяет делать надежные выводы на основе статистических данных. если у нас есть ряд данных, то для обоснованных выводов и надежных прогнозов на их основе, помимо средних значений, надо еще указать, насколько используемые данные различаются между собой.

Одним из статистических показателей различия или разброса данных является размах.

Размах — это разность между наибольшим и наименьшим значениями ряда данных.

Eсть более удобный способ нахождения среднего арифметического, а также других статистических характеристик — составление таблицы частот.

Для того чтобы составить таблицу частот, нужно для каждого числа из данного ряда посчитать, сколько раз данное число встречается в этом ряду. Затем полученные данные внести в таблицу, в первой колонке которой — число заболеваний за год, а во второй — количество появлений этого числа заболеваний в ряде данных (частота).

Теперь, для того чтобы найти среднее арифметическое членов исходного ряда, уже не понадобится складывать подряд все числа ряда. Можно догадаться, что для этого нужно каждое из чисел первой колонки умножить на частоту его появления в ряду, сложить все получившиеся произведения, а затем поделить результат на общее количество данных (сумму всех частот). Итак, в данном случае среднее арифметическое будет равно.

Таким образом, мы получили тот же самый результат за меньшее количество действий, что очень важно, особенно для больших рядов с повторяющимися данными.

Из таблицы частот сразу можно найти и моду ряда данных (напомним, что мода наиболее часто встречающееся в ряду число). Таким образом, мы получили тот же самый результат за меньшее количество действий, что очень важно, особенно для больших рядов с повторяющимися данными.

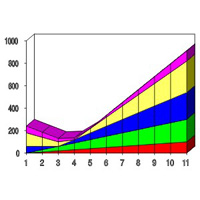
Из таблицы частот сразу можно найти и моду ряда данных (напомним, что мода наиболее часто встречающееся в ряду число).

Еще одной важной статистической характеристикой ряда данных является его медиана. Обычно медиану ищут в случае, когда числа в ряду являются какими-либо показателями и надо найти, например, человека, показавшего средний результат, фирму со средней годовой прибылью, авиакомпанию, предлагающую средние цены на билеты, и т. д.

Медианой ряда, состоящего из нечетного количества чисел, называется число данного ряда, которое окажется посередине, если этот ряд упорядочить. Медианой ряда, состоящего из четного количества чисел, называется среднее арифметическое двух стоящих посередине чисел этого ряда.

наверх